1. 기대수익률과 위험
1.1 투자 성향 분석 가이드 라인
- 금융 상품을 가입하기 전에 투자 정보확인서 작성 : 고객의 투자 성향 확인
- 투자 성향 검사 항목
- 항목별 점수를 이용한 개인 종합 점수 계산
- 점수에 따른 투자 성향 파악 : 5가지 유형 (안정형, 안정추구형, 위험중립형, 적극투자형, 공격투자형 등)
1.2 기대수익률과 위험
1) 투자 자산
- 미래의 불확실한 현금 흐름
2) 기대 수익률
- 미래 수익률의 기대치, 평균
- 기대수익률 = 기대수익/투자금액 $ = {E[P_1] - P_0 \over P_0} = E[r] $
- 예) 기대수익 ≠ 실현수익률(사후수익률) $ = {P_1 - P_0 \over P_0} $
3) 위험 (Risk)
- 미래 수익률의 변동성 (Volatility), 분산 또는 표준편차
- $ Var(r) = E[(r-E[r])^2] $
- 예) 불확실성 (uncertainty) $ \ne Risk \ne Danger $
1.3 투자 자산의 가치
- 각 투자 자산은 기대수익률과 위험에 의해서 구분 : $Value(A)=f(E[r_A],\sigma_A^2)$
- 평균 : $E(r) = \sum r_i p_i$
- 분산 : $Var(r) = \sigma^2 = \sum [r_i - E(r)]^2 p_i = E(r^2) - [E(r)]^2 $
- 표준편차 : $\sigma = \sqrt{Var(r)}$

- Q) 예제 : (현재) 1,000만원씩 주식에 투자 → (1년 후) 가치/확률은 각각 1,300만원(30%), 1,100만원(40%), 900만원(30%)
A1) 각각의 투자수익률은?
- 투자수익률 $ = {1,300 - 1,000 \over 1,000} = 0.3 $
- 투자수익률 $ = {1,100 - 1,000 \over 1,000} = 0.1 $
- 투자수익률 $ = {900 - 1,000 \over 1,000} = -0.1 $
A2) 평균은?
- $ E[r] = {\sum r_i P_i } = 0.3 \times 0.3 + 0.1 \times 0.4 - 0.1 \times 0.3 = 0.1 $
A3) 분산은?
$$ \begin{align} Var(r) &= \sigma^2 = {\sum [r_i - E(r)]^2} p_i \\ &= (0.3-0.1)^2 \times 0.3 + (0.1-0.1)^2 \times 0.4 + (-0.1-0.1)^2 \times 0.3 \end{align}$$
A4) 표준편차는?
- $ \sigma = \sqrt{Var(r)} $
2. 포트폴리오의 위험분산 효과
2.1 포트폴리오의 기대수익률과 위험
1) 포트폴리오란?
- 위험을 분산하고 투자수익을 극대화하기 위하여 여러 종목으로 나누어 투자한 자산 묶음
- 포트폴리오 $ P = \alpha A + \beta B, \alpha + \beta = 1 $
- 예1) 포트폴리오1 = 0.2×정기예금 + 0.3×채권 + 0.4×주식 + 0.1×부동산
- 예2) 포트폴리오2 = 0.5×정기예금 + 0.5×부동산
2) 포트폴리오의 기대수익률
$ E(\alpha r_A + \beta r_B ) = \alpha E(r_A) + \beta E(r_B) $
$ E[r_p] = $ 자산A의 구성비율 × 자산A의 기대수익률 + 자산B의 구성비율 × 자산B의 기대수익률
3) 포트폴리오의 위험
$ Var(r_A + r_B) = Var(r_A) + Var(r_B) + 2Cov(r_A, r_B) $
$ Var(\alpha r_A + \beta r_B) = \alpha^2 Var(r_A) + \beta^2 Var(r_B) + 2\alpha \beta Cov(r_A, r_B) $
$ Var(r_p) = $ (자산A의 구성비율2 × 자산A의 분산) + (자산B의 구성비율2 × 자산B의 분산) + ( 2 × 자산A의 구성비율 × 자산B의 구성비율 × 공분산)
4) 자산 사이의 공분산
- $ Cov(r_A, r_B) = E[r_A - E(r_A)][r_B - E(r_B)] = E(r_A r_B) - E(r_A) E(r_B) $
- $ Cov(r_A, r_B) = $ (자산A의 편차 × 자산B의 편차 × 확률)의 총합
$$ \begin{align} Var(r_A + r_B ) &= Var(r_A ) + Var(r_B ) + 2Cov(r_A , r_B ) \\ &= Var(r_A ) + Var(r_B ) + 2Corr(r_A , r_B ) \sqrt{Var(r_A )} \sqrt{Var(r_B )} \end{align} $$
- 상관계수 : $ Corr(r_A , r_B ) = \rho_AB = { Cov(r_A , r_B ) \over \sqrt{ Var(r_A ) } \sqrt{ Var(r_B ) } } $
$ Var(\alpha r_A + \beta r_B ) = \alpha^2 Var(r_A ) + \beta^2 Var(r_B ) + 2\alpha \beta Cov(r_A , r_B ) $
$ Cov(\alpha r_A , \beta r_B ) = \alpha \beta Cov(r_A , r_B ) $
5) 예제
- Q1) 자산A와 B의 수익률 확률분포가 아래와 같을 때, 각 자산의 기대수익률과 분산, 표준편차 구하기
| 상황 | 확률 | 수익률 | |
| 자산A | 자산B | ||
| 호황 | 0.4 | 0.30 | 0.10 |
| 불황 | 0.6 | 0.05 | 0.15 |
$ S = { 1 = $ 호황, $ , 2 = $ 불황 $ }, p(1) = 0.4, p(2) = 0.6$
자산 A의 경우, $ r_A (1) = 0.3, r_A (2) = 0.05 $
$ E(r_A ) = p(1)r_A (1) + p(2) r_A (2) = 0.4 \times 0.3 + 0.6 \times 0.05 = 0.15 $
$$ \begin{align} Var(r_A ) &= p(1)[r_A (1) - E(r_A (1))]^2 + p(2)[r_A (2) - E(r_A (2))]^2 \\ &= 0.4 \times (0.3 - 0.15)^2 + 0.6 \times (0.05-0.15)^2 = 0.015 \end{align} $$
$ SD(r_A ) = \sqrt{0.015} = 0.1225 $
자산 B의 경우, $ r_B (1) = 0.1, r_B (2) = 0.15 $
$ E(r_B ) = 0.13, Var(r_B ) = 0.0006, SD(r_B ) = 0.0245 $
- Q2) 자산A와 B 각각 50%로 구성된 포트폴리오의 기대수익률 및 분산 구하기
$ I = {A, B}, \alpha = 0.5, \beta = 0.5 $
$ E(r_p ) = \alpha E[r_A ] + \beta E[r_B ] = 0.5 \times 0.15 + 0.5 \times 0.13 = 0.14 $
$ Cov(r_A , r_B ) = 0.4 \times (0.3-0.15)(0.1-0.13) + 0.6 \times (0.05-0.15)(0.15-0.13) = -0.003 $
$ \rho_{AB} = { Cov(r_A r_B ) \over \sigma_A \times \sigma_B } = - {0.003 \over 0.1225} \times 0.0245 = -1 $
$ Var(r_p ) = 0.5^2 \times 0.015 + 0.5^2 \times 0.0006 + 2 \times 0.5 \times 0.5 \times (-0.003) = 0.0024 $
$ SD(r_p ) = \sqrt{0.0024} = 0.04899 $
2.2 상관계수와 위험분산 효과
- 상관계수 ↓ → 위험 ↓ (위험분산 효과 ↑)
- 상관관계가 낮은 자산들을 결합한 경우, 포트폴리오의 위험분산 효과는 증가함
- 일정한 기대수익률 하에서 위험 감소효과 극대화
1) 상관계수 : $ Corr(r_A , r_B ) = \rho_AB = { Cov(r_A ,r_B ) \over \sqrt {Var(r_A )} \sqrt {Var(r_B ) } } $
- 공분산을 각 투자안의 표준편차로 나누어 표준화한 값. 각 투자안 수익률의 상관관계를 보다 분명하게 측정할 수 있도록 나타낸 것
- 두 자산의 상관계수가 -1 일 때, 특정 구성비율에 따라 포트폴리오를 구성하면 위험을 완전히 제거할 수 있음
- $ -1 \le \rho_AB \le 1 $
- $ \rho_AB = 0 $ 인 경우 : 두 투자안의 수익률이 독립적으로 움직임
- $ \rho_AB = 1 $ 인 경우 : 두 투자안의 수익률이 양(+)의 기울기를 갖는 완전한 직선 관계
- $ \rho_AB = -1 $ 인 경우 : 두 투자안의 수익률이 음(-)의 기울기를 갖는 완전한 직선 관계

2) 포트폴리오 p의 분산을 공분산과 상관계수 관계를 이용하여 정리
$ Var(r_p ) = $ (자산A의 구성비율2 × 자산A의 분산) + (자산B의 구성비율2 × 자산B의 분산) + (2 × 자산A의 구성비율 × 자산B의 구성비율 × 자산A의 표준편차 × 자산B의 표준편차 × 상관계수)
2.3 구성 자산의 수와 위험분산 효과
구성자산의 수 ↑ → 포트폴리오의 위험 ↓ (위험분산효과 ↑)
자산의 총위험
= 체계적 위험 + 비체계적 위험
= 분산 불가능 위험 + 분산 가능 위험
= 시장 위험 + 개별 위험
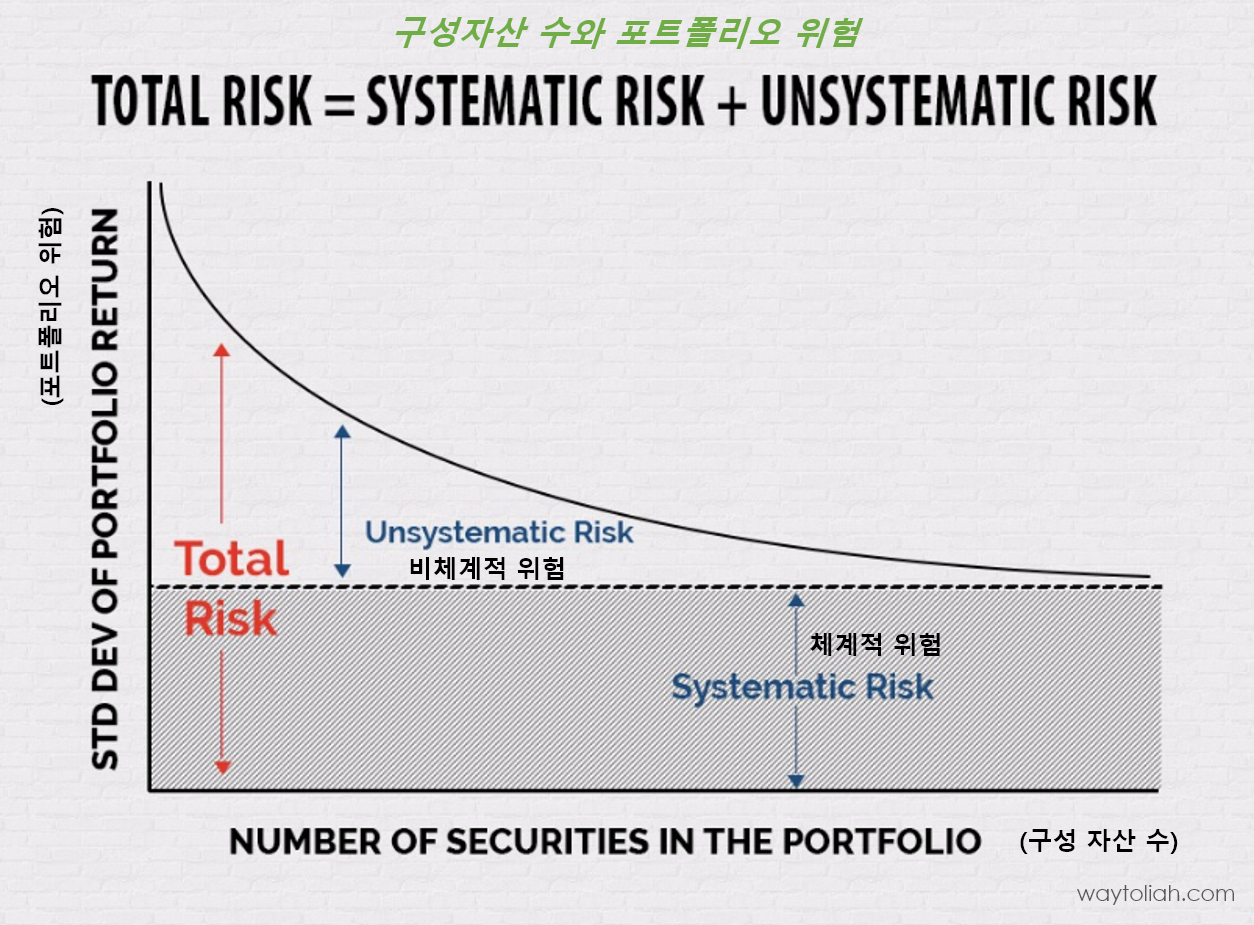
2.4 위험 관리
- 계란을 한 바구니에 담지 마라 - Don't put all your eggs in one basket !

3. 위험과 기대수익률의 관계
3.1 자본자산 가격결정 이론 (CAPM, Capital asset pricing model)
1) CAPM이란?
- 현대 금융 이론 핵심이론
- 기업의 가치를 계산하거나 자산에 대한 투자 결정을 보조할 때 가장 많이 사용되는 재무 모델 (금융 실무에서 압도적으로 많이 사용됨)
- CAPM은 투자자들이 평균-분산 기준 (mean-variance criterion)에 따라 각자의 기대효용을 극대화할 수 있는 최적 포트폴리오를 선택하는 경우 자본시장의 균형 상태에서 위험 자산의 가격이 어떻게 결정되는가 하는 것을 설명하는 모형
- CAPM은 해리 마코위츠(Harry Markowitz, 1952)의 포트폴리오 이론(portfolio selection theory)을 확대 · 발전시킨 모형으로 윌리엄 샤프(William Sharpe, 1964), 린트너(J. Lintner, 1965), 모신(J. Mossin, 1966) 등에 의해 개발 → 1990년 마코위츠 & 샤프는 노벨경제학상 수상
2) CAPM을 이용한 기업가치평가
- 시장 변동성과 해당 주식의 변동성을 기반으로 베타($\beta $)를 구한 후 요구수익률을 산출
- 기업의 과거 상황(재무제표 기준)과, 현재 상황(기업구조, 유·무형 가치 등)을 바탕으로 기업의 성장성을 예측
- 성장성을 바탕으로 미래 기업으로부터 얻어질 가치 계산
- 해당 가치를 요구수익률로 할인
3.2 CAPM : 자본시장선 (CML, Capital Market Line)
1) 자본시장선 (CML, Capital market line) 이란?
$ E(r_p ) = r_f + [ { E(r_m ) - r_f \over \sigma_M } ] = \sigma_p $
- $ E(r_p ) $ : 효율적 포트폴리오의 기대수익률
- $ r_f $ : 무위험이자율
- $ E(r_M ) $ : 시장포트폴리오 기대수익률
- $ \sigma_M $ : 시장포트폴리오 수익률의 표준편차
- $ \sigma_p $ : 효율적 포트폴리오 수익률의 표준편차
- 효율적 포트폴리오 기대수익률과 위험의 선형 관계를 나타내는 직선
- 기대수익률 = 무위험이자율 + (위험의 균형가격) × (위험) = 무위험이자율 + 위험 프리미엄
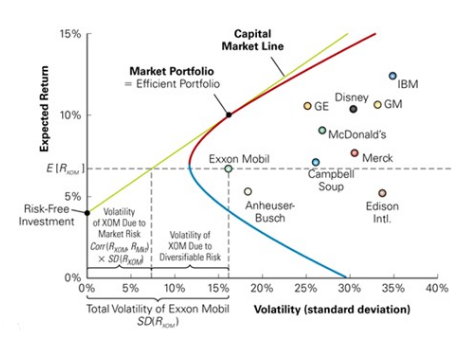
2) 자본시장선(CML) 예제 : 무위험이자율이 5%이고, 시장포트폴리오의 기대수익률이 20%, 표준편차라 10%라고 할 때, 자본시장선 구하기
- $ E(r_p ) = r_f + [ { E(r_M ) - r_f \over \sigma_M } ] \sigma_p $ 이므로
- $ E(r_p ) = 0.05 + [ { 0.2 - 0.05 \over 0.1 } ] \sigma_p = 0.05 + 1.5 \sigma_p $
3.3 CAPM : 증권시장선 (SML, Security Market Line)
1) 증권시장선 (SML, Security market line) 이란?
$ E(r_j ) = r_f + [E(r_M ) -r_f ] \beta_j $
- $ E(r_j ) $ : 자산 j의 기대수익률
- $ r_f $ : 무위험이자율
- $ E(r_M ) $ : 시장포트폴리오 기대수익률
- 모든 위험자산의 기대수익률과 체계적 위험의 선형 관계를 나타내는 직선
- 개별 증권의 기대수익률 = 무위험이자율 + (시장위험 프리미엄) × (체계적 위험) = 무위험이자율 + 위험 프리미엄
- 체계적 위험 척도: 베타($\beta $)
- $ \beta_j = $ 자산j와 시장포트폴리오의 공분산 / 시장포트폴리오의 분산 = $ { cov(r_j, r_M ) \over var(r_M ) } $
- 개별 증권 또는 포트폴리오의 수익이 증권시장 전체의 움직임에 대해서 얼마나 민감하게 반응해 변동하는 가를 나타내는 수치

2) 증권시장선 (SML) 예제 : 무위험이자율이 8%이며, 시장수익률이 10%로 기대될 때 증권시장선 구하기. 베타가 1.5인 증권 K의 기대수익률 구하기
- A1) 증권시장선
- $ E(r_j ) = r_f + [E(r_M ) - r_f ] \beta_j $ 이므로
- $ E(r_j ) = 0.08 + [ 0.10 - 0.08 ] \beta_j = 0.08 + 0.02 \beta_j $
- A2) 베타가 1.5인 증권 k의 기대수익률
- $ E(r_k ) = 0.08 + 0.02 × 1.5 = 0.11 (11%) $
3.4 CML과 SML의 비교
| 자본시장선 (CML) | 증권시장선 (SML) | ||
| 동일한 점 | 기대수익률과 위험의 선형 관계를 보여 줌 | ||
| 차이점 | 평가 대상 | 무위험 자산, 시장 포트폴리오 |
개별 주식, 효율적 포트폴리오, 비효율적 포트폴리오 |
| 위험 | 총위험 (표준편차) | 체계적 위험 (베타) | |
# 정리하기
- 투자자산의 미래 현금흐름의 특성은 기대치로 측정될 수 있으며, 평균과 분산(또는 표준편차)이라는 기초통계량으로 표현됨
- 평균은 미래에 기대되는 수익률의 평균수익률, 분산은 수익률이 평균에서 벗어난 정도를 측정
- 분산(또는 표준편차)은 위험의 측도로 사용. 개별 자산들의 합으로 포트폴리오를 구성할 경우, 기대수익률과 분산은 기대치 연산에 의해 계산되는데, 특히 위험을 나타내는 분산의 경우 개별 자산의 분산과 공분산의 합으로 구성됨.
- 공분산이 양의 값이라면 두 자산수익률이 평균적으로 같은 방향으로 움직이고, 공분산이 음의 값이라면 두 자산수익률이 평균적으로 다른 방향으로 움직임을 의미
- 투자자가 포트폴리오를 구성하려는 이유는 일정한 기대수익률 하에서 투자위험을 최소화할 수 있는 포트폴리오의 위험분산효과에 의해 설명될 수 있음.
- 일반적으로는 구성자산들 간의 상관계수가 작을수록, 포트폴리오의 위험분산효과가 크게 나타남
- 자산수익률의 분산(총위험)은 포트폴리오의 구성자산 수를 증가시킴에 따라 제거할 수 있는 부분, 즉 비체계적 위험과 제거할 수 없는 부분, 즉 체계적 위험으로 구성됨
- 따라서 구성자산의 수가 많을수록 위험분산효과는 커지게 됨
- 자본자산가격결정모형(CAPM)은 자산의 위험과 기대수익률 사이에 어떠한 관계가 성립하여야 하는가를 보여주는 이론 모형
- CAPM에 따르면, 모든 투자자들이 보유하는 위험자산의 최적포트폴리오는 시장포트폴리오(market portfolio: M)
- 최적포트폴리오란 투자자의 기대효용을 가장 극대화시켜 주는 포트폴리오로, 자본시장선 상의 시장포트폴리오와 무위험자산의 결합으로 이루어짐
- 시장포트폴리오는 시장에서 거래되는 모든 위험자산이 시장가치 비율대로 구성되어 있는 포트폴리오
- 자본시장선(CML)이란 효율적 포트폴리오의 기대수익률과 위험 사이의 선형관계를 나타낸 것
- CAPM에 따르면, 균형 하에서 개별 자산(또는 포트폴리오)의 기대수익률이 그 자산의 체계적 위험의 지표인 베타계수와 선형적 관계를 가지고 있는데, 이러한 관계를 증권시장선(SML)이라 한다.
- 즉, 자본시장이 균형을 이룰 때 어떤 자산의 가격은 그 자산에 대한 기대수익률과 위험 사이에 선형적 관계가 성립하도록 자산가격이 결정되는데, 이 때의 가격이 그 자산에 대한 수요와 공급을 일치시키는 균형가격임
- 베타($\beta =$ 자산 i와 시장포트폴리오의 공분산 / 시장포트폴리오의 분산)는 시장수익률의 변동에 대한 개별자산의 민감도를 나타냄
- 이에 따라 개별자산의 위험프리미엄은 시장포트폴리오의 위험프리미엄과 그 자산의 체계적 위험을 나타내는 베타계수에 비례함
방송대 경제학과, 재테크와 금융투자 - 강의 노트 정리
'Financial Story > 재테크 기본 이론' 카테고리의 다른 글
| [재테크와 금융투자] ⑤ 금융상품의 선택기준 (0) | 2021.09.17 |
|---|---|
| [파생금융상품] 선물(Futures) · 옵션(Options) 거래 Essential (0) | 2021.09.09 |
| [재테크와 금융투자] ③ 금융경제학 이론 Ⅰ : 화폐와 시간 가치 (0) | 2021.08.25 |
| [재테크와 금융투자] ② 산업의 성장과 금융시스템 (1) | 2021.08.21 |
| [재테크와 금융투자] ① 재테크와 금융투자의 기초개념 (1) | 2021.08.20 |



